Higher-order convergence algorithm for reciprocal and square root
Takayuki HOSODA
Nov. 16, 2009
example of sqrt(2) by Newton-Raphson method

The Newton-Raphson method is a first-order approximation of a function f(x) around the approximate value of xn .
Its convergence speed can be increased by higher order approximation.

Japanese Japanese edition is here.

Reciprocal

The recurrence formula for reciprocal 1 / A by Newton-Raphson method is Given by
Xn+1 = 2 * Xn - A * Xn2
The significant digit is Doubles with each iteration.

Since the calculation time of multiplication is dominant in the calculation with a large number of digits, in order to reduce the number of multiplications required to obtain the calculation result of the required number of digits, it is desirable to use a recurrence formula that converges in a higher order.

Recurrence formula for 1 / A of cubic convergence
hn = 1 - A * xn
xn+1 = xn * (1 + hn + hn2)

The number of significant digits is tripled with each repetition. hn is equal to the error of xn .
Recurrence formula for 1 / A of fourth-order convergence
hn = 1 - A * xn
xn+1 = xn * (1 + hn) * (1 + hn2)
Recurrence formula for 1 / A of fifth-order convergence
hn = 1 - A * xn
xn+1 = xn * (1 + (1 + hn2) * (hn + hn2))

Square root

A similar method can be applied to the square root calculation. The recurrence formula by the Newton-Raphson method for √A (square root of A) is given by,
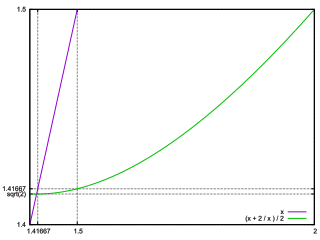
Xn+1 = (Xn + A / Xn) / 2
However, this formula has the disadvantage of having to perform each A / Xn division, which requires a lot of computation time.
Then, when we consider the Newton-Raphson method of 1 / √A, we find that a better recurrence formulas are obtained.

Recurrence formula for 1 / √A by Newton-Raphson method
Xn+1 = Xn * (3 - A * Xn2) / 2
That is, the above equation (since 3/2 and 1/2 are constants) only requires multiplication.
To find √A, find 1 / √A and then √A = A * (1 / √A) to find √A.
To find 1 / √A, it is better to use the recurrence formula of higher-order convergence, as in the case of the reciprocal calculation above.
Here we use a series expansion of 1 / √(1 - h).

Recurrence formula for 1 / √A of cubic convergence
hn = 1 - A * xn2
xn+1 = xn * (1 + hn * (4 + 3 * hn) / 8)

The number of significant digits is tripled with each repetition. hn is equal to the error of xn .
Recurrence formula for 1 / √A of fourth-order convergence
hn = 1 - A * xn2
xn+1 = xn * (1 + hn * (8 + hn * (6 + 5 * hn)) / 16)
Recurrence formula for 1 / √A of fifth-order convergence
hn = 1 - A * xn2
xn+1 = xn * (1 + (64 * hn + hn2 * (48 + 40 * hn + 35 * hn2)) / 128)
Recurrence formula for 1 / √A of 6th-order convergence
hn = 1 - A * xn2
xn+1 = xn * (1 + hn * (1/2 + hn * (3/8 + hn * (5/16 + hn * (35/128 + hn * 63/256)))))

Appendix ‐ Other recurrence formulas of 6th-order convergence

As in the case of 1 / √A, we use the series expansion of √(1 - h) .

Recurrence formula for √A of 6th-order convergence
hn = 1 - A / xn2
xn+1 = xn * (1 - hn * (1/2 + hn * (1/8 + hn * (1/16 + hn * (5/128 + hn * 7/256)))))

Recurrence formula for 1 / ∛A of 6th-order convergence
hn = 1 - A * xn3
xn+1 = xn + xn * hn * (1/3 + hn * (2/9 + hn * (14/81 + hn * (35/243 + hn * 91/729))))

Recurrence formula for 1 / ∜A of 6th-order convergence
hn = 1 - A * xn4
xn+1 = xn + xn * hn * (1/4 + hn * (5/32 + hn * (15/128 + hn * (195/2048 + hn * 663/8192))))

A program example

Example of a C program with fourth-order convergence to find √x 
#include <stdio.h>
#include <math.h>
#ifndef DBL_EPSILON
#define DBL_EPSILON     2.2204460492503131E-16
#endif

double
_sqrtinv(a)
    double a;
{
    double x, h, g;
    int    e;

    /* enhalf the exponent for a half digit initial accuracy */
    frexp(a, &e);
    x = ldexp(1.0, -e >> 1);

    /* 1/sqrt(a), fourth-order convergence */
    g = 1.0;
    while(fabs( h = 1.0 - a * x * x) < fabs(g)) {
        x += x * (h * (8.0 + h * (6.0 + 5.0 * h)) / 16.0);
        g = h;
    }
    return(x);
}

double
sqrt(a)
    double(a);
{
    if(a < 0){
        fprintf(stderr, "sqrt: domain error\n");
        return(0);
    }
    return(a * _sqrtinv(a));
}
*note1 : It is better to expand the loop as current processors can calculate the contents while determining the jump condition of the loop. If the machine ε is about 10-16, three calculations are enough.
SEE ALSO:
www.finetune.co.jp [Mail]