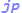very_long_float
pi2(iter)
int iter;
{
int i;
very_long_float a, b, t, x, y;
a = 1;
b = 1 / sqrt(2);
t = 1;
x = 4;
for (i = 0; i < iter; i++) {
y = a;
a = (a + b) / 2;
b = sqrt(y * b);
t -= x * sqr(y - a);
x *= 2;
}
return (sqr(a + b) / t);
}
(但し、sqr(x) は x2, sqrt(x) は x1/2)
この公式は2次の収束を示し、n桁の答えが log
very_long_float
pi(iter)
int iter;
{
int i;
very_long_float a, b, y, t;
y = sqrt(2) - 1;
a = 6 - sqrt(32);
b = 8;
for (i = 0; i < iter; i++) {
t = qroot(1 - pow4(y));
y = (1 - t) / (1 + t);
t = sqr(1 + y);
a = sqr(t) * a - y * (t - y) * b;
b *= 4;
}
return (1 / a);
}
(但し、sqr(x) は x2, pow4(x) は x4, sqrt(x) は x1/2, qroot(x) は x1/4)
この公式は4次の収束を示し、繰り返しごとの誤差は次のようになる。

![[Mail]](/~lyuka/images/mail.gif)