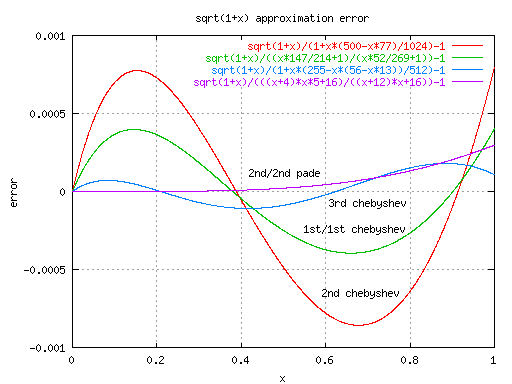
Fig.1 sqrt(1+x) の近似誤差参考プログラムを下に示す。
very_long_float hypotenuse(p, q) very_long_float p; very_long_float q; { very_long_float r, x, h; p = fabs(p); q = fabs(q); if (p == 0) return(q); if (q == 0) return(p); if(p < q) { r = p; p = q; q = r; } r = q / p; r *= r; x = 1 + r * (500 - r * 77) / 1024; /* 2nd order chebyshev approximation (|err| < 0.09 %) */ /* Other approximations. * x = (129 + r * 53) / 128; chebyshev[1] (|err| < 1 %) * x = (x * 147 / 214 + 1) / (x * 52 / 269 + 1); chebyshev[1,1] (|err| < 0.04%) * x = ((r + 4) * r * 5 + 16) / ((r + 12) * r + 16); pade[2,2] (|err| < 0.03%) * x = 1 + r * (255 - r * (56 - r * 13)) / 512; chebyshev[3] (|err| < 0.02%) */ r += 1; while(fabs(h = 1 - r / (x * x)) > VLF_EPSILON){ x *= 1 - h * (128 + h * (32 + h * (16 + h * (10 + h * 7))))/256; /* Taylor series*/ /* Altanative: Pade[2,2] approximation. (6th order convergence) * x *= 1 - h * ((h - 12) * h + 16) / ((6 * h - 32) * h + 32); */ } return(p * x); }
Fig.2 1/sqrt(1+x) の近似誤差収束の様子と誤差の例
very_long_float hypotenuse(p, q) very_long_float p; very_long_float q; { very_long_float r, x, h; p = fabs(p); q = fabs(q); if (p == 0) return(q); if (q == 0) return(p); if(p < q) { r = p; p = q; q = r; } r = q / p; r *= r; x = (1021 + r * (r * 149 - 444)) / 1024; /* chebyshev[2] (err < 0.38%) */ r += 1; while(fabs(h = 1 - r * x * x) > VLF_EPILON){ x += x * (h * (128 + h * (96 + h * (80 + h * (70 + h * 63))))/256); } return(p * x * r); }
hypotenuse の語源はギリシャ語の hupo (下) + teinousa (伸) だそうです。
#ifndef M_SQRT2 #define M_SQRT2 1.4142135623730950488 #endif double _hypot(x, y) double x; double y; { register double a; register double b; x = fabs(x); y = fabs(y); if(x == 0) return(y); if(y == 0) return(x); if(y > x) { a = x; x = y; y = a; } a = x - y; if(a > y){ a = x / y; a += sqrt(1.0 + a * a); }else{ a /= y; b = a * (a + 2.0); a += b / (M_SQRT2 + sqrt(2.0 + b)); a += M_SQRT2 + 1.0; } return(x + y / a); }
C. B. Moler and D. Morrison, IBM Journal of Research and Development 27(6), 577-581, 1983

![[Mail]](/~lyuka/images/mail.gif)



 © 2000 Takayuki HOSODA.
© 2000 Takayuki HOSODA.