パデ近似(Padé approximant)

パデ近似(Padé approximant)

ある有理関数のべき級数展開が、あるべき級数の最大次数まで一致するとき、それはパデ近似と呼ばれる。

パデ近似 (Padé approximant)

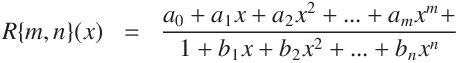
$R\{m, n\}(x) = \frac{a_0 + a_1 x + a_2 x^2 + ... + a_m x^m} {1 + b_1 x b_2 x^2 + ... + b_n x^n}$

として、
$R(0) &=& f(0)\\ \displaystyle\frac{d^k}{d x^k}R(x)\:| \:_{x = 0} &=& \displaystyle\frac{d^k}{d x^k}f(x) \:| \:_{x = 0,\, k = 1, , ,\,m + n}$

が成り立つ (即ち f (x) と R(x) の x = x₀ でのテーラー級数 (Taylor series) が m + n 次の項まで一致する) ならば、 R(x) は f (x) のパデ近似と呼ばれる。

例

R{1, 1}(x) = (a + b x) / (c + d x)
として、

f(x) = ln(1 + x) / x = 1 - x / 2 + x² / 3 - x³ / 4 + …
の a, b, c, d の値を未定係数として求める。
R{1, 1}(0) = f(0) = 1
より、
a / c = 1
↓
a = c
であるので、
R'{1, 1}(0) = f'(0) = -1 / 2

(b c - a d) / c² = (b - d) / c = -1 / 2
↓
b = (2d - c) / 2
それから、また、
R''{1, 1}(0) = f''(0) = 2 / 3

2 ( a d² - b c d) / c³ = 2 / 3
↓
b = c / 6
d = 2c / 3

全ての係数が整数になるように c = 6 に選ぶと、
a = c = 6
b = c / 6 = 1
d = 2 c / 3 = 4

R{1, 1}(x) = (6 + x) / (6 + 4 x)

こうして得られたパデ近似と、もとのべき級数近似の様子を Fig.1 に示す。
Fig.1 ln(1 + x) / x とその近似

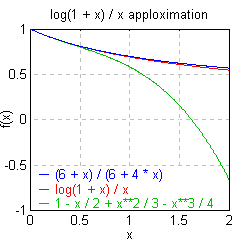
べき級数による近似は x が大きいところで発散しているが、パデ近似は x が大きいところでも良い近似になっている。

外部リンク

Padé approximant — Wikipedia
パデ(Padé)近似 — Wolfram

パデ近似 (Padé approximant)

例

関連項目

外部リンク