グレゴリオ暦とバイナリ暦

グレゴリオ暦は、 ローマ教皇グレゴリウス13世が 西暦 1582年2月24日 に発令したものだそうだが、１年を 365.2425 日とし、 端数を 97/400 で近似したため、誤差の補正がややこしい。
それに加え、実際の太陽年が 365.24219 ^*1と結構違う （もちろん当時の観測技術からすればコペルニクス等は偉大であって 非があるわけではない）ため悩ましいことになっている。

うるう年 なんてのは、つまるところ１年の端数の分数近似の問題なのである。
今日の測定技術で得られている 太陽年 365.24219 の端数をあらためて分数近似してみると次のような結果が得られる。

[table.1 0.24219 の分数近似]

近似値	誤差
1 / 4	+0.03224740905900325
7 / 29	-0.003347329184410608
8 / 33	+0.0009671845420637926
31 / 128	-1.032247409049614e-05
752 / 3105	+6.648936601294508e-08
4543 /18758	-4.40237712950875e-09

ここで、 31/128 に着目すると、これは　2^5 - 1 / 2^ 7 であるから技術的に （というか 2進数的に）大変都合が良い。
確か似たようなことを小林芳直さんがどこかに書かれていて、 これを「バイナリ暦」と提唱(笑)されていた記憶があるので、ここでも バイナリ暦（Binarian）と呼ぶことにする(笑)。
即ち 128 で割り切れず 4 で割り切れる年をうるう年にすればよく、 これだけで数十万年の間はややこしいい他の補正をせずとも誤差が １日以内に収まることになる。

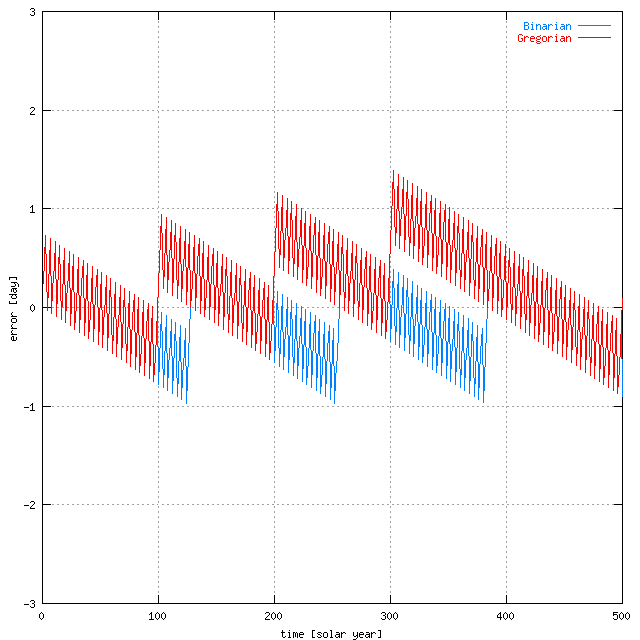
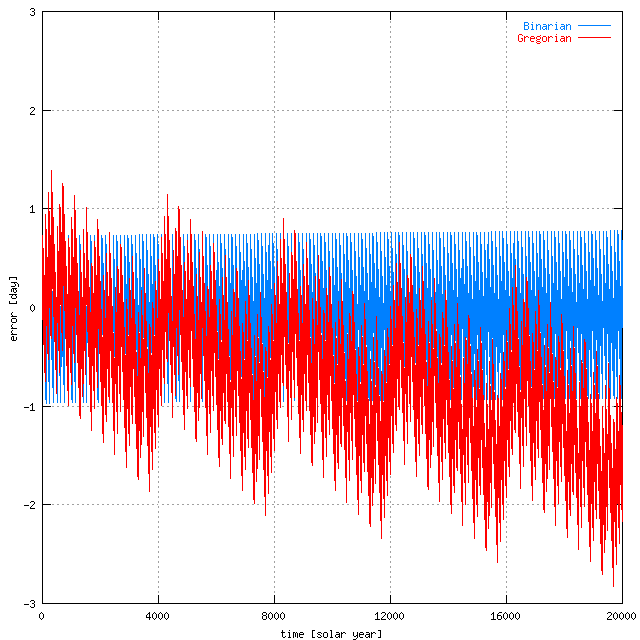
下のグラフは Binarian が、西暦で表した年が 128 で割り切れず 4 で割り切れる年を うるう年とした場合の太陽年とのずれ。
Gregorian が、西暦で表した年が 100　で割り切れず 4 で割り切れる年を うるう年とし、4000 で割り切れ 400 で割り切れない年も閏年とした場合の太陽年とのずれ。

128 年で割り切れる上、２進数で下位ビットが全部 '0' の年 2048 年がまもなく （といっても 42 年後^*2だが）やってくる。
この文字通り千載一遇の機会に、 宗教的見地からでなく 科学・技術的見地から 是非とも暦法が変更されないものかなと、
ツーリング先の三保の松原で日の出を望みながら夢想するのである。