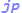Karatsuba method

Karatsuba 法^{^*1}による乗算

筆算の方法で n 桁の乗算を行うには Ο n² の計算量が必要であるが、 Karatsuba法では Ο n^log₂3 の計算量で計算できる。
数千桁を越える乗算の場合にはＦＦＴや中国人剰余定理による乗算が望ましい。

n 桁の数 X と Y の積を求める。

まず、X, Y を上位 n / 2 桁と下位 n / 2 に分割し

X = a R + b
Y = c R + d

と表現すると

X Y = (a R + b) (c R + d)
    =  a c R² + (a d + b c) R + b d … (1)

ところで

(a - b) (c - d) =  a c - (a d + b c) + b d

であるから、

(a d + b c) =  a c + b d - (a - b)(c - d) … (2)

(1) に (2) を代入して

X Y = a c R² + (a c + b d - (a - b)(c - d)) R + b d … (3)

となり、n 桁の数の掛け算が n/2 桁の数の３つの掛け算の和に分解できた。
つまり、桁数が２倍になったときに乗算の計算量が３倍で済むということである。

【10進 6桁の数の掛け算の例】

X = 123456
Y = 789012
X を上位３桁と、下位３桁に分けて
a = 123
b = 456
Y を上位３桁と、下位３桁に分けて
c = 789
d =  12
a c = 97047
b d =  5472
(a - b)(c - d) = -258741

X Y = 97047*1000000 + (97047 + 5472 + 258741)*1000 + 5472

   97047
  +   97047
  +    5472
  +  258741
  +       5472
--------------         
   97408265472

Note

*1: 以前は２分割法と記載していたが、一般的には発見者 Anatolii Alexeevitch Karatsuba (ロシア語: Карацуба, Анатолий Алексеевич) の名前をとって Karatsuba 法と呼ぶらしく、記載を改めた。

SEE ALSO: 中国人剰余定理を利用した数値計算の例