HP 35s trigonometric functions alternative

HP 35s trigonometric functions (tan, cos and sin) alternative

Takayuki HOSODA (a.k.a Lyuka)

The HP 35s's built-in trigonometric functions seems to lose its accuracy around ±π/2, ±&pi/4, ±π3/2 and so on. In some case its accuracy goes down to seven digits or less which is not acceptable as the scientific calculator that features internal 15 digits precision. Anyway as it was necessary, I wrote the alternative trigonometric functions for the HP 35s. [Aug. 30, 2007]

Usage


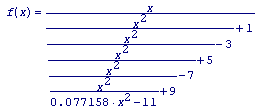
SIN(χ) : [XEQ] [SIN] [ENTER]
COS(χ) : [XEQ] [COS] [ENTER]

TAN(χ) : [XEQ] [TAN] [ENTER]

Resources to be used

MEM I   : Index, π
MEM J   : Work memory
MEM 0   : X register storage
MEM 1   : Y register storage
MEM 2   : Z register storage
MEM 3   : T register storage
MEM 4   : Anchor
FLAG 1  : χ < 0
FLAG 2  : π/4 < |χ| < 3/4·π
FLAG 3  : π/2 < |χ|
FLAG 4  : π < |χ|

Features

The input χ is to be in radian, and the usable input range would be |x| < 100 or so.
The 11.5 digits precision can be expected.
All the contents of Y, Z and T registers are preserved, and the input value in the X register will be saved to the LASTχ register.

List 1 [ Trigonometrics functions program ]

Calculate sin(χ) Calculate cos(χ) tangent→cosine conversion Calculate tan(χ) Restore registers Save registers Range reduction tangent approximation

H001 LBL H
H002 XEQ J015
H003 χ<>y
H004 XEQ I006
H005 FS? 3
H006 +/-
H007 XEQ J004
H008 RTN

I001 LBL I
I002 XEQ J015
I003 XEQ I006
I004 XEQ J004
I005 RTN


I006 i1
I007 ×
I008 +
I009 LASTχ
I010 χ<>y
I011 ÷
I012 ABS
I013 FS? 3
I014 +/-
I015 FS? 4
I016 +/-
I017 RTN

J001 LBL J
J002 XEQ J015
J003 ÷


J004 3
J005 STO I
J006 CLχ
J007 RCL(I)
J008 DSE I
J009 GTO J007
J010 R↑
J011 χ<>(I)
J012 ABS
J013 χ<>(I)
J014 RTN


J015 RPN
J016 STO J
J017 CLχ
J018 4
J019 STO I
J020 STO(I)
J021 DSE I
J022 R↑
J023 STO(I)
J024 DSE I
J025 GTO J022 
J026 RCL J
J027 STO(I)


J028 CF 1
J029 SF 2
J030 CF 3
J031 CF 4
J032 χ<0?
J033 SF 1
J034 ABS
J035 ENTER
J036 ENTER
J037 π
J038 STO I
J039 RMDR
J040 χ<>y
J041 LASTχ
J042 INT÷
J043 STO J
J044 2
J045 RMDR
J046 χ≠0?
J047 SF 4
J048 R↓
J049 0.25
J050 RCL× I
J051 χ<y?
J052 CF 2
J053 CLχ
J054 0.5
J055 RCL× I
J056 x≤y?
J057 SF 3
J058 CLχ
J059 0.75
J060 RCL× I
J061 χ<>y
J062 χ<y?
J063 GTO J068
J064 SF 2
J065 RCL- I
J066 ISG J
J067 2007 09/06
J068 FS? 2
J069 GTO J078
J070 ENTER
J071 +
J072 RCL- I
J073 0.5
J074 ×
J075 LASTχ
J076 STO+ J
J077 CLχ
J078 2.06761537357E-13
J079 RCL× J
J080 +


J081 STO J
J082 χ²
J083 ENTER
J084 ENTER
J085 ENTER
J086 7.7158e-2
J087 ×
J088 11
J089 -
J090 ÷
J091 9
J092 +
J093 ÷
J094 7
J095 -
J096 ÷
J097 5
J098 +
J099 ÷
J100 3
J101 -
J102 ÷
J103 1
J104 +
J105 RCL J
J106 χ<>y
J107 FS? 2
J108 GTO J111
J109 +/-
J110 χ<>y
J111 FS? 1
J112 +/-
J113 RTN

Note

The execution of the program never reaches the line J067 and is to be used as the revision date code.
The checksum is not shown here as a checksum is meaningless on the HP 35s because of its bug.
[2007 08/31] Modified to store π into the valiable I to reduse line steps.
[2007 09/06] Modified to use complex number operation to convert tangent to sine and cosine.
[2015 08/03] Missing two lines (H005 and H006) are corrected. Thanks to Gerald H at MoHPC

The modified 13th order continued fraction (shown below) is used as the approximation of the tangent.
One coefficient had been optimized for the range [-π/4 ≤ χ ≤ π/4].
It's worth to use the optimized value 0.077158 instead of 1/13(=0.07692307~) as the last coefficient of the continued fraction,
since this slight change of the coefficient greatly improve (about 24 times better) the worst approximation error.

equ.1 [ The approximate expression of the tangent ]

Its theoretical relative error is within ± 7.5e-15. ("13th ContFrac/Opt1Comp" plot below.)

fig.1 [ The approximation errors of the tangent ]

Some complex number operations are used in the 'tangent→cosine conversion', since it cause less calculation error than that of the real number operation.

equ.2 [tangent to sine/cosine conversion]

Some calculation results (P.U.T. : Program Under Test (on the HP 35s))

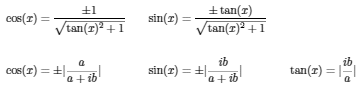
table.1 [ calculation results ]

Input [rad] cos(χ) sin(χ) tan(χ)

-4.71238898039 +5.310142306034~e-12 9.999999999999~e-1 +1.883188702614~e11 actual

-4.71238898039 +5.31014230603e0 +1.00000000000e0 +1.88318870261e11 HP 35s built-in

-4.71238898039 +5.31014230604e0 +1.00000000000e0 +1.88318870261e11 P.U.T.

-4.71238898038 -4.689857693965~e0 9.999999999999~e-1 -2.132260860040~e11 actual

-4.71238898038 -4.68985769397e0 +1.00000000000e0 -2.13226086004e11 HP 35s built-in

-4.71238898038 -4.68985769396e0 +1.00000000000e0 -2.13226086004e11 P.U.T.

-3.14159265359 -0.999999999999~e0 +2.067615373566~e-13 -2.067615373566~e-13 actual

-3.14159265359 -1.00000000000e0 +2.06761537357e-13 -2.06761537357e-13 HP 35s built-in

-3.14159265359 -1.00000000000e0 +2.06761537357e-13 -2.06761537357e-13 P.U.T.

-2.35619449019 -7.071067811848~e-1 -7.071067811882~e-1 +1.00000000000~e0 actual

-2.35619449019 -7.07106781185e-1 -7.07106781188e-1 +1.00000000001e0 HP 35s built-in

-2.35619449019 -7.07106781184e-1 -7.07106781189e-1 +1.00000000001e0 P.U.T.

-1.57079632680 -5.103380768678~e-12 -9.9999999999999~e-1 +1.959485379059~e11 actual

-1.57079632680 -5.10338076868e-12 -1.000000000000e0 +1.95948537906e11 HP 35s built-in

-1.57079632680 -5.10338076868e-12 -1.000000000000e0 +1.95948537906e11 P.U.T.

-1.57079632679 +4.896619231321~e-12 -9.9999999999999~e-1 -2.042225365622~e11 actual

-1.57079632679 +4.89661923132e-12 -1.00000000000e0 -2.04222536562e11 HP 35s built-in

-1.57079632679 +4.89661923132e-12 -1.00000000000e0 -2.04222536562e11 P.U.T.

-.785398163398 +7.071067811861~e-1 -7.071067811861~e-1 -1.000000000001~e0 actual

-.785398163398 +7.07106781186e-1 -7.07106781187e-1 -1.00000000000e0 HP 35s built-in

-.785398163398 +7.07106781186e-1 -7.07106781187e-1 -1.00000000000e0 P.U.T.

-.523598775598 +8.660254037845~e-1 -4.999999999997~e-1 -5.773502691892~e-1 actual

-.523598775598 +8.66025403785e-1 -5.00000000000e-1 -5.77350269189e-1 HP 35s built-in

-.523598775598 +8.66025403784e-1 -5.00000000000e-1 -5.77350269189e-1 P.U.T.

0.000000000000 +1 0 0 actual

0.000000000000 +1.00000000000e0 0.000000000000e0 0.00000000000e0 HP 35s built-in

0.000000000000 +1.00000000000e0 0.000000000000e0 0.00000000000e0 P.U.T.

+.000010000000 +9.999999999500~e-1 +9.999999999833~e-6 +1.000000000033~e-5 actual

+.000010000000 +9.99999999950e-1 +9.99999999950e-6 +1.00000000000e-5 HP 35s built-in

+.000010000000 +9.99999999950e-1 +9.99999999983e-6 +1.00000000003e-5 P.U.T.

+.000100000000 +9.999999950000~e-1 +9.999999983333~e-5 +1.000000003333~e-4 actual

+.000100000000 +9.99999995000e-1 +9.99999998300e-5 +1.00000000330e-4 HP 35s built-in

+.000100000000 +9.99999995000e-1 +9.99999998333e-5 +1.00000000333e-4 P.U.T.

+.001000000000 +9.999995000000~e-1 +9.99999833333~e-4 +1.000000333333~e-3 actual

+.001000000000 +9.99999500000e-1 +9.99999833330e-4 +1.00000033333e-3 HP 35s built-in

+.001000000000 +9.99999500000e-1 +9.99999833333e-4 +1.00000033333e-3 P.U.T.

+.010000000000 +9.999500004166~e-1 +9.999833334166~e-3 +1.000033334666~e-2 actual

+.010000000000 +9.99950000417e-1 +9.99983333416e-3 +1.00003333467e-2 HP 35s built-in

+.010000000000 +9.99950000416e-1 +9.99983333417e-3 +1.00003333467e-2 P.U.T.

+.100000000000 +9.950041652780~e-1 +9.983341664682~e-2 +1.003346720854~e-1 actual

+.100000000000 +9.95004165278e-1 +9.98334166468e-2 +1.00334672085e-1 HP 35s built-in.

+.100000000000 +9.95004165278e-1 +9.98334166468e-2 +1.00334672085e-1 P.U.T.

+.500000000000 +8.775825618903~e-1 +4.7942553860420~e-2 +5.46302489843~e-1 actual

+.500000000000 +8.77582561890e-1 +4.79425538604e-2 +5.46302489844e-1 HP 35s built-in.

+.500000000000 +8.77582561890e-1 +4.79425538604e-2 +5.46302489844e-1 P.U.T.

+.730300000000 +7.449743079245~e-1 +6.670931573119~e-1 +8.954579375635~e-1 actual

+.730300000000 +7.44974307925e-1 +6.67093157312e-1 +8.95457937564e-1 HP 35s built-in

+.730300000000 +7.44974307925e-1 +6.67093157312e-1 +8.95457937564e-1 P.U.T.

+.785398163397 +7.071067811868~e-1 +7.071067811862~e-1 +9.999999999991e-1 actual

+.785398163397 +7.07106781187e-1 +7.07106781186e-1 +9.99999999999e-1 HP 35s built-in

+.785398163397 +7.07106781187e-1 +7.07106781186e-1 +9.99999999999e-1 P.U.T.

+.785398163398 +7.071067811861~e-1 +7.071067811869~e-1 +1.000000000001~e0 actual

+.785398163398 +7.07106781186e-1 +7.07106781187e-1 +1.00000000000e0 HP 35s built-in

+.785398163398 +7.07106781186e-1 +7.07106781187e-1 +1.00000000000e0 P.U.T.

+1.00000000000 +5.403023058681~e-1 +8.414709848078~e-1 +1.557407724654~e0 actual

+1.00000000000 +5.40302305868e-1 +8.41470984808e-1 +1.55740772465e0 HP 35s built-in

+1.00000000000 +5.40302305869e-1 +8.41470984808e-1 +1.55740772465e0 P.U.T.

+1.57079632000 +6.794896619231~e-9 +9.999999999999e-1 +1.471692736530~e8 actual

+1.57079632000 +6.79489000000e-9 +1.00000000000e0 +1.47169417018e8 HP 35s built-in

+1.57079632000 +6.79489661923e-9 +1.00000000000e0 +1.47169273653e8 P.U.T.

+1.57079632679 +4.896619231321~e-12 +9.999999999999~e-1 +2.042225365622~e11 actual

+1.57079632679 +4.89661923132e-12 +1.00000000000e0 +2.04222536562e11 HP 35s built-in

+1.57079632679 +4.89661923132e-12 +1.00000000000e0 +2.04222536562e11 P.U.T.

+1.57079632680 -5.103380768678~e-12 +9.999999999999~e0 -1.959485379059~e11 actual

+1.57079632680 -5.10338076868e-12 +1.00000000000e0 -1.95948537906e11 HP 35s built-in

+1.57079632680 -5.10338076868e-12 +1.00000000000e0 -1.95948537906e11 P.U.T.

+1.57079640000 -7.320510338076~e-8 +9.999999999999~e-1 -1.366024981617~e7 actual

+1.57079640000 -7.32051000000e-8 +1.00000000000e0 -1.36602504470e7 HP 35s built-in

+1.57079640000 -7.32051033808e-8 +1.00000000000e0 -1.36602498162e-7 P.U.T.

+2.00000000000 -4.161468365471~e-1 +9.092974268256~e-1 -2.185039863261~e0 actual

+2.00000000000 -4.16146836547e-1 +9.09297426826e-1 -2.18503986326e0 HP 35s built-in

+2.00000000000 -4.16146836547e-1 +9.09297426826e-1 -2.18503986326e0 P.U.T.

+3.00000000000 -9.899924966004~e-1 +1.4112000805986~e-1 -1.425465430742~e-1 actual

+3.00000000000 -9.89992496600e-1 +1.41120008060e-1 -1.42546543074e-1 HP 35s built-in

+3.00000000000 -9.89992496600e-1 +1.41120008060e-1 -1.42546543075e-1 P.U.T.

+3.14159260000 -9.999999999999~e-1 +5.358979323846~e-8 -5.358979323846~e-8 actual

+3.14159260000 -1.00000000000e0 +5.35897900000e-8 -5.35897900000e-8 HP 35s built-in

+3.14159260000 -1.00000000000e0 +5.35897932385e-8 -5.35897932385e-8 P.U.T.

+3.14159266000 -9.999999999999~e-1 -6.410206761537~e-9 +6.410206761537~e-9 actual

+3.14159266000 -1.00000000000e0 -6.41020000000e-9 +6.41020000000e-9 HP 35s built-in

+3.14159266000 -1.00000000000e0 -6.41020676154e-9 +6.41020676154e-9 P.U.T.

+4.00000000000 -6.536436208636~e-1 -7.568024953079~e-1 +1.157821282349~e0 actual

+4.00000000000 -6.53643620864e-1 -7.56802495308e-1 +1.15782128235e0 HP 35s built-in

+4.00000000000 -6.53643620864e-1 -7.56802495308e-1 +1.15782128235e0 P.U.T.

+4.71238900000 +1.961531014230~e-8 -9.999999999999~e-9 -5.098058571315~e7 actual

+4.71238900000 +1.96153100000e-8 -1.00000000000e-0 -5.09805860830e7 HP 35s built-in

+4.71238900000 +1.96153101423e-8 -1.00000000000e0 -5.09805857132e7 P.U.T.

+5.00000000000 +2.836621854632~e-1 -9.589242746631~e-1 -3.380515006246~e0 actual

+5.00000000000 +2.83662185463e-1 -9.58924274663-1 -3.38051500625e0 HP 35s built-in

+5.00000000000 +2.83662185462e-1 -9.58924274663-1 -3.38051500625e0 P.U.T.

+6.00000000000 +9.601702866503~e-1 -2.794154981989~e-1 -2.910061913847~e-1 actual

+6.00000000000 +9.60170286650e-1 -2.79415498199-1 -2.91006191385e-1 HP 35s built-in

+6.00000000000 +9.60170286650e-1 -2.79415498200-1 -2.91006191385e-1 P.U.T.

+10.0000000000 -8.390715290764~e-1 -5.440211108893~e-1 +6.483608274590~e-1 actual

+10.0000000000 -8.39071529076e-1 -5.44021110889e-1 +6.48360827459e-1 HP 35s built-in

+10.0000000000 -8.39071529077e-1 -5.44021110889e-1 +6.48360827459e-1 P.U.T.

+355.000000000 -9.999999995456~e-1 -3.014435335948~e-5 +3.014435337318~e-5 actual

+355.000000000 -9.99999999546e-1 -3.01443533555e-5 +3.01443533692e-5 HP 35s built-in

+355.000000000 -9.99999999546e-1 -3.01443533595e-5 +3.01443533732e-5 P.U.T.

REFERENCE

Fast and Accurate Trigonometric Functions on the HP-12C Platinum
Fast and Accurate Trigonometric Functions on the HP-17BII

EXTERNAL LINKS

http://www.hp.com/calculatores/ - HP calculators
http://www.hpmuseum.org/ - The Museum of HP calculators
The Museum of HP calculators/HP Articles Forum/735 : HP-35s bug list

Input [rad]	cos(χ)	sin(χ)	tan(χ)
-4.71238898039	+5.310142306034~e-12	9.999999999999~e-1	+1.883188702614~e11	actual
-4.71238898039	+5.31014230603e0	+1.00000000000e0	+1.88318870261e11	HP 35s built-in
-4.71238898039	+5.31014230604e0	+1.00000000000e0	+1.88318870261e11	P.U.T.
-4.71238898038	-4.689857693965~e0	9.999999999999~e-1	-2.132260860040~e11	actual
-4.71238898038	-4.68985769397e0	+1.00000000000e0	-2.13226086004e11	HP 35s built-in
-4.71238898038	-4.68985769396e0	+1.00000000000e0	-2.13226086004e11	P.U.T.
-3.14159265359	-0.999999999999~e0	+2.067615373566~e-13	-2.067615373566~e-13	actual
-3.14159265359	-1.00000000000e0	+2.06761537357e-13	-2.06761537357e-13	HP 35s built-in
-3.14159265359	-1.00000000000e0	+2.06761537357e-13	-2.06761537357e-13	P.U.T.
-2.35619449019	-7.071067811848~e-1	-7.071067811882~e-1	+1.00000000000~e0	actual
-2.35619449019	-7.07106781185e-1	-7.07106781188e-1	+1.00000000001e0	HP 35s built-in
-2.35619449019	-7.07106781184e-1	-7.07106781189e-1	+1.00000000001e0	P.U.T.
-1.57079632680	-5.103380768678~e-12	-9.9999999999999~e-1	+1.959485379059~e11	actual
-1.57079632680	-5.10338076868e-12	-1.000000000000e0	+1.95948537906e11	HP 35s built-in
-1.57079632680	-5.10338076868e-12	-1.000000000000e0	+1.95948537906e11	P.U.T.
-1.57079632679	+4.896619231321~e-12	-9.9999999999999~e-1	-2.042225365622~e11	actual
-1.57079632679	+4.89661923132e-12	-1.00000000000e0	-2.04222536562e11	HP 35s built-in
-1.57079632679	+4.89661923132e-12	-1.00000000000e0	-2.04222536562e11	P.U.T.
-.785398163398	+7.071067811861~e-1	-7.071067811861~e-1	-1.000000000001~e0	actual
-.785398163398	+7.07106781186e-1	-7.07106781187e-1	-1.00000000000e0	HP 35s built-in
-.785398163398	+7.07106781186e-1	-7.07106781187e-1	-1.00000000000e0	P.U.T.
-.523598775598	+8.660254037845~e-1	-4.999999999997~e-1	-5.773502691892~e-1	actual
-.523598775598	+8.66025403785e-1	-5.00000000000e-1	-5.77350269189e-1	HP 35s built-in
-.523598775598	+8.66025403784e-1	-5.00000000000e-1	-5.77350269189e-1	P.U.T.
0.000000000000	+1	0	0	actual
0.000000000000	+1.00000000000e0	0.000000000000e0	0.00000000000e0	HP 35s built-in
0.000000000000	+1.00000000000e0	0.000000000000e0	0.00000000000e0	P.U.T.
+.000010000000	+9.999999999500~e-1	+9.999999999833~e-6	+1.000000000033~e-5	actual
+.000010000000	+9.99999999950e-1	+9.99999999950e-6	+1.00000000000e-5	HP 35s built-in
+.000010000000	+9.99999999950e-1	+9.99999999983e-6	+1.00000000003e-5	P.U.T.
+.000100000000	+9.999999950000~e-1	+9.999999983333~e-5	+1.000000003333~e-4	actual
+.000100000000	+9.99999995000e-1	+9.99999998300e-5	+1.00000000330e-4	HP 35s built-in
+.000100000000	+9.99999995000e-1	+9.99999998333e-5	+1.00000000333e-4	P.U.T.
+.001000000000	+9.999995000000~e-1	+9.99999833333~e-4	+1.000000333333~e-3	actual
+.001000000000	+9.99999500000e-1	+9.99999833330e-4	+1.00000033333e-3	HP 35s built-in
+.001000000000	+9.99999500000e-1	+9.99999833333e-4	+1.00000033333e-3	P.U.T.
+.010000000000	+9.999500004166~e-1	+9.999833334166~e-3	+1.000033334666~e-2	actual
+.010000000000	+9.99950000417e-1	+9.99983333416e-3	+1.00003333467e-2	HP 35s built-in
+.010000000000	+9.99950000416e-1	+9.99983333417e-3	+1.00003333467e-2	P.U.T.
+.100000000000	+9.950041652780~e-1	+9.983341664682~e-2	+1.003346720854~e-1	actual
+.100000000000	+9.95004165278e-1	+9.98334166468e-2	+1.00334672085e-1	HP 35s built-in.
+.100000000000	+9.95004165278e-1	+9.98334166468e-2	+1.00334672085e-1	P.U.T.
+.500000000000	+8.775825618903~e-1	+4.7942553860420~e-2	+5.46302489843~e-1	actual
+.500000000000	+8.77582561890e-1	+4.79425538604e-2	+5.46302489844e-1	HP 35s built-in.
+.500000000000	+8.77582561890e-1	+4.79425538604e-2	+5.46302489844e-1	P.U.T.
+.730300000000	+7.449743079245~e-1	+6.670931573119~e-1	+8.954579375635~e-1	actual
+.730300000000	+7.44974307925e-1	+6.67093157312e-1	+8.95457937564e-1	HP 35s built-in
+.730300000000	+7.44974307925e-1	+6.67093157312e-1	+8.95457937564e-1	P.U.T.
+.785398163397	+7.071067811868~e-1	+7.071067811862~e-1	+9.999999999991e-1	actual
+.785398163397	+7.07106781187e-1	+7.07106781186e-1	+9.99999999999e-1	HP 35s built-in
+.785398163397	+7.07106781187e-1	+7.07106781186e-1	+9.99999999999e-1	P.U.T.
+.785398163398	+7.071067811861~e-1	+7.071067811869~e-1	+1.000000000001~e0	actual
+.785398163398	+7.07106781186e-1	+7.07106781187e-1	+1.00000000000e0	HP 35s built-in
+.785398163398	+7.07106781186e-1	+7.07106781187e-1	+1.00000000000e0	P.U.T.
+1.00000000000	+5.403023058681~e-1	+8.414709848078~e-1	+1.557407724654~e0	actual
+1.00000000000	+5.40302305868e-1	+8.41470984808e-1	+1.55740772465e0	HP 35s built-in
+1.00000000000	+5.40302305869e-1	+8.41470984808e-1	+1.55740772465e0	P.U.T.
+1.57079632000	+6.794896619231~e-9	+9.999999999999e-1	+1.471692736530~e8	actual
+1.57079632000	+6.79489000000e-9	+1.00000000000e0	+1.47169417018e8	HP 35s built-in
+1.57079632000	+6.79489661923e-9	+1.00000000000e0	+1.47169273653e8	P.U.T.
+1.57079632679	+4.896619231321~e-12	+9.999999999999~e-1	+2.042225365622~e11	actual
+1.57079632679	+4.89661923132e-12	+1.00000000000e0	+2.04222536562e11	HP 35s built-in
+1.57079632679	+4.89661923132e-12	+1.00000000000e0	+2.04222536562e11	P.U.T.
+1.57079632680	-5.103380768678~e-12	+9.999999999999~e0	-1.959485379059~e11	actual
+1.57079632680	-5.10338076868e-12	+1.00000000000e0	-1.95948537906e11	HP 35s built-in
+1.57079632680	-5.10338076868e-12	+1.00000000000e0	-1.95948537906e11	P.U.T.
+1.57079640000	-7.320510338076~e-8	+9.999999999999~e-1	-1.366024981617~e7	actual
+1.57079640000	-7.32051000000e-8	+1.00000000000e0	-1.36602504470e7	HP 35s built-in
+1.57079640000	-7.32051033808e-8	+1.00000000000e0	-1.36602498162e-7	P.U.T.
+2.00000000000	-4.161468365471~e-1	+9.092974268256~e-1	-2.185039863261~e0	actual
+2.00000000000	-4.16146836547e-1	+9.09297426826e-1	-2.18503986326e0	HP 35s built-in
+2.00000000000	-4.16146836547e-1	+9.09297426826e-1	-2.18503986326e0	P.U.T.
+3.00000000000	-9.899924966004~e-1	+1.4112000805986~e-1	-1.425465430742~e-1	actual
+3.00000000000	-9.89992496600e-1	+1.41120008060e-1	-1.42546543074e-1	HP 35s built-in
+3.00000000000	-9.89992496600e-1	+1.41120008060e-1	-1.42546543075e-1	P.U.T.
+3.14159260000	-9.999999999999~e-1	+5.358979323846~e-8	-5.358979323846~e-8	actual
+3.14159260000	-1.00000000000e0	+5.35897900000e-8	-5.35897900000e-8	HP 35s built-in
+3.14159260000	-1.00000000000e0	+5.35897932385e-8	-5.35897932385e-8	P.U.T.
+3.14159266000	-9.999999999999~e-1	-6.410206761537~e-9	+6.410206761537~e-9	actual
+3.14159266000	-1.00000000000e0	-6.41020000000e-9	+6.41020000000e-9	HP 35s built-in
+3.14159266000	-1.00000000000e0	-6.41020676154e-9	+6.41020676154e-9	P.U.T.
+4.00000000000	-6.536436208636~e-1	-7.568024953079~e-1	+1.157821282349~e0	actual
+4.00000000000	-6.53643620864e-1	-7.56802495308e-1	+1.15782128235e0	HP 35s built-in
+4.00000000000	-6.53643620864e-1	-7.56802495308e-1	+1.15782128235e0	P.U.T.
+4.71238900000	+1.961531014230~e-8	-9.999999999999~e-9	-5.098058571315~e7	actual
+4.71238900000	+1.96153100000e-8	-1.00000000000e-0	-5.09805860830e7	HP 35s built-in
+4.71238900000	+1.96153101423e-8	-1.00000000000e0	-5.09805857132e7	P.U.T.
+5.00000000000	+2.836621854632~e-1	-9.589242746631~e-1	-3.380515006246~e0	actual
+5.00000000000	+2.83662185463e-1	-9.58924274663-1	-3.38051500625e0	HP 35s built-in
+5.00000000000	+2.83662185462e-1	-9.58924274663-1	-3.38051500625e0	P.U.T.
+6.00000000000	+9.601702866503~e-1	-2.794154981989~e-1	-2.910061913847~e-1	actual
+6.00000000000	+9.60170286650e-1	-2.79415498199-1	-2.91006191385e-1	HP 35s built-in
+6.00000000000	+9.60170286650e-1	-2.79415498200-1	-2.91006191385e-1	P.U.T.
+10.0000000000	-8.390715290764~e-1	-5.440211108893~e-1	+6.483608274590~e-1	actual
+10.0000000000	-8.39071529076e-1	-5.44021110889e-1	+6.48360827459e-1	HP 35s built-in
+10.0000000000	-8.39071529077e-1	-5.44021110889e-1	+6.48360827459e-1	P.U.T.
+355.000000000	-9.999999995456~e-1	-3.014435335948~e-5	+3.014435337318~e-5	actual
+355.000000000	-9.99999999546e-1	-3.01443533555e-5	+3.01443533692e-5	HP 35s built-in
+355.000000000	-9.99999999546e-1	-3.01443533595e-5	+3.01443533732e-5	P.U.T.