Arithmetic-Geometric Mean
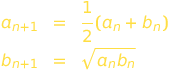
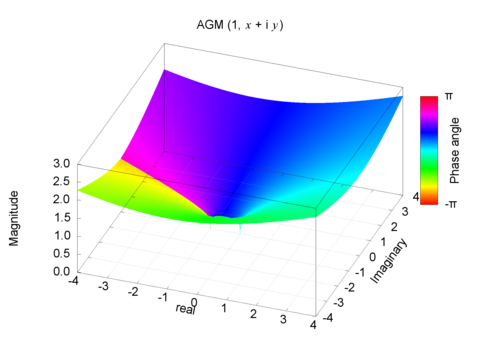
Jan. 8 2023
Takayuki HOSODA
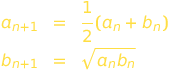

The arithmetic-geometric mean can be used to compute - among others - logarithms, complete and incomplete elliptic integrals of the first and second kind, and Jacobi elliptic functions.
OperationInput
Resources used
Output
Download : cagm.raw — (raw program file for Free42)
Arithmetic-Geometric Mean - for HP 42S
Rev.1.0 (Jan. 8, 2023) (c) 2022 Takayuki HOSODA00 { 158-Byte Prgm } 01▸LBL "cAGM" ; for complex number arguments 02 0 03 ENTER 04 0 05 COMPLEX 06 X=Y? 07 RTN 08 R↓ 09 X<>Y 10 R↑ 11 X=Y? 12 RTN 13 RCL ST Z 14 RCL+ ST Z 15 X=Y? 16 RTN 17 R↓ 18 R↓ 19 ENTER 20 ABS 21 RCL ST Z 22 ABS 23 X>Y? 24 X<>Y 25 CLX 26 2?-12 27 × 28 STO 00 29▸LBL 00 30 R↓ 31 ENTER 32 RCL× ST Z 33 SQRT 34 ENTER 35 R↓ 36 RCL+ ST Y 37 ABS 38 STO 01 39 CLX 40 RCL ST T 41 RCL- ST Y 42 ABS 43 R↓ 44 + 45 0.5 46 × 47 LASTX 48 R↑ 49 RCL- 01 50 X>0? 51 GTO 02 52 X≠0? 53 GTO 03 54 CLX 55 RCL ST T 56 RCL÷ ST Y 57 X<>Y 58 R↓ 59 COMPLEX 60 X≤0? 61 GTO 03 62▸LBL 02 63 R↑ 64 +/- 65 R↓ 66▸LBL 03 67 R↓ 68 R↓ 69 ENTER 70 RCL- ST Z 71 ABS 72 RCL- 00 73 X>0? 74 GTO 00 75 R↓ 76 + 77 0.5 78 × 79 RTN 80▸LBL "AGM" ; for real number arguments 81 0 82 COMPLEX 83 X<>Y 84 0 85 COMPLEX 86 XEQ "cAGM" 87 COMPLEX 88 X=0? 89 GTO 01 90 COMPLEX 91 RTN 92▸LBL 01 93 R↓ 94 RTN 95 .END.
1 ENTER 2 XEQ "AGM" → 1.45679103105 1 ENTER .25 XEQ "AGM" → 5.60757145072e-1 2 +/- ENTER 2 COMPLEX 1 ENTER 0 COMPLEX XEQ "cAGM" → 1.26420344318e-2 +1.32391495927i 3 +/- ENTER 2 COMPLEX 2 +/- ENTER 2 COMPLEX XEQ "cAGM" → -2.48482321791 +2.01232838848i 1 ENTER 2 COMPLEX 3 ENTER 4 COMPLEX +/- XEQ "cAGM" → -2.05175259566 +7.24586986859e-2i 1.5 ENTER 2 COMPLEX +/- 3 ENTER 4 COMPLEX XEQ "cAGM" → 1.95698167954 -1.45966858375e-1i
agm(1, 2) ~= 1.4567910310469068691864323832650819749738639432213055907941723832... agm(1, 0.25) ~= 0.5607571450719006425319505482072666351272432856016524939797059253... agm(-2 + 2 i, 1) ~= 0.012642034431775224871144882985098306376405625767985282751139254... + 1.3239149592728229110180317045523087521571829295502353536455198... i agm(-3 + 2 i, -2 + 2 i) ~= -2.48482321791345966540888302608455218648014162219542779589616405... + 2.01232838847582894914613621798033481637378492177117070798341113... i agm(1 + 2 i, -3 - 4 i) ~= -2.051752595659329572693583864239458955398878779423072275607602... + 0.07245869868588149813029197687616500840652284108968969453100464... i agm(-1.5 - 2i, 3 + 4 i) ~= 1.95698167953681205998137584021754054093691534541639368664817292... - 0.145966858375103771971664986222696913809981322179346508693130731... i

![[Mail]](/~lyuka/images/mail.gif)



 © 2000 Takayuki HOSODA.
© 2000 Takayuki HOSODA.